Cate_marketing_credit_case_study
📘 Conditional Average Treatment Error (CATE) & Treatment Heterogeneity
Demonstration with Marketing & Credit data, including comments
This notebook mirrors the ideas from the chapter 5 of Facure’s Causal analytics book:
- Effect heterogeneity: different units respond differently to the same intervention.
- CATE: treatment effect conditional on context/features.
- Evaluation when you can’t observe individual effects:
- Effect-by-quantile plots
- Cumulative effect curves
- Cumulative gain curves (+ AUC)
- Ordering vs calibration: ranking is often what matters for decisions.
- Target transformation / pseudo-outcomes: an MSE-like comparison tool.
- Decision-making: treat top‑K/top‑p% where benefit is largest.
Because OpenML access can fail (firewall/outage), this notebook has two paths:
Path A — Real public datasets (requires internet)
Loads via sklearn.datasets.fetch_openml:
bank-marketing(marketing)credit-g(credit)
Path B — Automatic fallback (no internet required)
If download fails, it generates a synthetic mixed-type dataset and still runs end‑to‑end, producing all evaluation figures.
Public dataset references
- Bank Marketing (OpenML): https://www.openml.org/search?type=data&status=active&id=1461
- German Credit / credit-g (OpenML): https://www.openml.org/d/31
0) Imports and stable data loading
We use fetch_openml (scikit-learn) for stable public data access + caching.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import OneHotEncoder, StandardScaler
from sklearn.impute import SimpleImputer
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
np.random.seed(42)
plt.rcParams["figure.figsize"] = (9, 5)
1) Helper functions (chapter evaluation tools)
Key chapter constraint:
Individual treatment effects are unobservable, so evaluation must be group-based.
We implement:
- effect within a group (difference in means)
- effect-by-quantile
- cumulative effect
- cumulative gain + AUC
- pseudo-outcome + weighted MSE
def effect_binary(df: pd.DataFrame, y: str = "y", t: str = "t") -> float:
treated = df.loc[df[t] == 1, y]
control = df.loc[df[t] == 0, y]
if len(treated) == 0 or len(control) == 0:
return np.nan
return treated.mean() - control.mean()
def effect_by_quantile(df: pd.DataFrame, score_col: str, q: int = 10, y: str = "y", t: str = "t") -> pd.DataFrame:
quant = pd.qcut(df[score_col], q=q, labels=False, duplicates="drop")
rows = []
for k in sorted(quant.dropna().unique()):
g = df.loc[quant == k]
rows.append({
"quantile": int(k),
"n": len(g),
"score_mean": g[score_col].mean(),
"effect": effect_binary(g, y=y, t=t)
})
return pd.DataFrame(rows).sort_values("score_mean")
def cumulative_effect_curve(df: pd.DataFrame, score_col: str, steps: int = 100, y: str = "y", t: str = "t"):
df_sorted = df.sort_values(score_col, ascending=False).reset_index(drop=True)
n = len(df_sorted)
cutoffs = np.linspace(max(1, n // steps), n, steps).astype(int)
cutoffs = np.unique(np.clip(cutoffs, 1, n))
x = 100 * cutoffs / n
effects = [effect_binary(df_sorted.iloc[:c], y=y, t=t) for c in cutoffs]
return x, np.array(effects)
def cumulative_gain_curve(df: pd.DataFrame, score_col: str, steps: int = 100, y: str = "y", t: str = "t", normalize: bool = True):
x, ce = cumulative_effect_curve(df, score_col, steps=steps, y=y, t=t)
p = x / 100.0
ate = effect_binary(df, y=y, t=t)
gain = p * (ce - ate) if normalize else p * ce
auc = np.trapezoid(gain, p)
return x, gain, auc, ate
def pseudo_outcome_transformed(y, t, e, clip=1e-3):
e = np.clip(e, clip, 1 - clip)
return (t * y / e) - ((1 - t) * y / (1 - e))
def weighted_mse(y_true, y_pred, w):
return np.average((y_true - y_pred) ** 2, weights=w)
2) Load OpenML datasets (or fallback)
If OpenML fails, we generate a synthetic dataset that still supports:
- categorical + numeric columns
- a binary label
- realistic prevalence
This ensures the notebook runs even without internet.
def load_openml_or_fallback(name: str, fallback_n: int = 20000, seed: int = 0):
rng = np.random.default_rng(seed)
try:
data = fetch_openml(name=name, as_frame=True)
X = data.data.copy()
y_raw = data.target.copy()
return X, y_raw, "openml"
except Exception as e:
n = fallback_n
X = pd.DataFrame({
"age": rng.integers(18, 80, size=n),
"income": rng.normal(60000, 20000, size=n).clip(5000, 200000),
"balance": rng.normal(1500, 1200, size=n).clip(0, 15000),
"channel": rng.choice(["branch", "web", "mobile", "call"], size=n, p=[0.2, 0.35, 0.35, 0.1]),
"segment": rng.choice(["A", "B", "C"], size=n, p=[0.3, 0.5, 0.2]),
"region": rng.choice(["NE", "MW", "S", "W"], size=n),
})
logit = (
-2.0
+ 0.015*(X["age"] - 40)
+ 0.00002*(X["income"] - 60000)
+ 0.0006*(X["balance"] - 1500)
+ (X["channel"].eq("mobile")*0.3).astype(float)
+ (X["segment"].eq("A")*0.2).astype(float)
)
p = 1 / (1 + np.exp(-logit))
y_raw = pd.Series(rng.binomial(1, p), name="y_raw")
return X, y_raw, f"fallback (OpenML error: {type(e).__name__})"
3) Simulate treatment + heterogeneous effect + observed outcome
We simulate a realistic observational setting:
- treatment is targeted using a propensity e(x)
- true effect tau(x) varies across feature profiles
- observed outcome shifts due to treatment by tau(x)
This creates a clean environment to test the chapter’s evaluation curves.
def make_preprocessor(X: pd.DataFrame):
cat_cols = X.select_dtypes(include=["object", "category"]).columns.tolist()
num_cols = X.select_dtypes(exclude=["object", "category"]).columns.tolist()
num_pipe = Pipeline([
("imputer", SimpleImputer(strategy="median")),
("scaler", StandardScaler())
])
cat_pipe = Pipeline([
("imputer", SimpleImputer(strategy="most_frequent")),
("onehot", OneHotEncoder(handle_unknown="ignore"))
])
return ColumnTransformer([
("num", num_pipe, num_cols),
("cat", cat_pipe, cat_cols)
])
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def simulate_uplift_problem(X: pd.DataFrame, y_raw_binary: pd.Series, seed: int = 0):
rng = np.random.default_rng(seed)
pre = make_preprocessor(X)
Z = pre.fit_transform(X)
w_prop = rng.normal(size=Z.shape[1])
z_prop = (Z @ w_prop).A1 if hasattr(Z, "A1") else (Z @ w_prop)
# propensity e(x)
e_true = sigmoid(0.6 * (z_prop / (np.std(z_prop) + 1e-9)))
t = rng.binomial(1, e_true)
# estimate e_hat
prop_model = Pipeline([
("pre", pre),
("clf", LogisticRegression(max_iter=300))
])
prop_model.fit(X, t)
e_hat = prop_model.predict_proba(X)[:, 1]
# heterogeneous effect tau(x)
w_tau = rng.normal(size=Z.shape[1])
z_tau = (Z @ w_tau).A1 if hasattr(Z, "A1") else (Z @ w_tau)
true_tau = 0.7 * sigmoid(z_tau / (np.std(z_tau) + 1e-9)) # [0, 0.7]
# baseline anchored to label prevalence + feature variation
p0 = float(np.clip(y_raw_binary.mean(), 1e-4, 1 - 1e-4))
base_logit = np.log(p0 / (1 - p0))
base_logit = base_logit + 0.25 * (z_prop / (np.std(z_prop) + 1e-9))
# observed outcome under treatment
logit = base_logit + t * true_tau
y = rng.binomial(1, sigmoid(logit))
df = X.copy()
df["y"] = y.astype(int)
df["t"] = t.astype(int)
df["e_hat"] = e_hat
df["true_tau"] = true_tau
return df
4) Build scores: Random vs Outcome vs CATE (T-learner)
rand_score: a placebo baseliney_score: predicts the outcome Y (not effect)cate_score: predicts uplift via two models (treated vs control)
def outcome_model_score(df: pd.DataFrame):
X = df.drop(columns=["y", "t", "e_hat", "true_tau"])
y = df["y"].values
pre = make_preprocessor(X)
model = RandomForestClassifier(n_estimators=300, min_samples_leaf=50, random_state=0, n_jobs=-1)
pipe = Pipeline([("pre", pre), ("model", model)])
pipe.fit(X, y)
return pipe.predict_proba(X)[:, 1]
def fit_outcome_model_subset(df_subset: pd.DataFrame):
X = df_subset.drop(columns=["y", "t", "e_hat", "true_tau"])
y = df_subset["y"].values
pre = make_preprocessor(X)
model = RandomForestClassifier(n_estimators=250, min_samples_leaf=50, random_state=0, n_jobs=-1)
pipe = Pipeline([("pre", pre), ("model", model)])
pipe.fit(X, y)
return pipe
def t_learner_cate_score(df: pd.DataFrame):
treated = df[df["t"] == 1]
control = df[df["t"] == 0]
m1 = fit_outcome_model_subset(treated)
m0 = fit_outcome_model_subset(control)
X_all = df.drop(columns=["y", "t", "e_hat", "true_tau"])
mu1 = m1.predict_proba(X_all)[:, 1]
mu0 = m0.predict_proba(X_all)[:, 1]
return mu1 - mu0
def add_scores(df: pd.DataFrame, seed: int = 0):
rng = np.random.default_rng(seed)
out = df.copy()
out["rand_score"] = rng.normal(size=len(out))
out["y_score"] = outcome_model_score(out)
out["cate_score"] = t_learner_cate_score(out)
return out
5) Plotting functions (clear figures)
def plot_effect_by_quantile(df, title, q=10):
plt.figure()
for s in ["rand_score", "y_score", "cate_score"]:
tab = effect_by_quantile(df, score_col=s, q=q)
plt.plot(tab["score_mean"], tab["effect"], marker="o", label=s)
plt.axhline(effect_binary(df), linestyle="--", color="black", label="ATE")
plt.xlabel("Mean score in quantile (low → high)")
plt.ylabel("Estimated effect within quantile")
plt.title(title)
plt.legend()
plt.show()
def plot_cumulative_effect(df, title):
plt.figure()
ate = effect_binary(df)
for s in ["rand_score", "y_score", "cate_score"]:
x, ce = cumulative_effect_curve(df, s, steps=80)
plt.plot(x, ce, label=s)
plt.axhline(ate, linestyle="--", color="black", label="ATE")
plt.xlabel("Top % of population (ranked by score)")
plt.ylabel("Effect among top-% subset")
plt.title(title)
plt.legend()
plt.show()
def plot_cumulative_gain(df, title):
plt.figure()
aucs = {}
for s in ["rand_score", "y_score", "cate_score"]:
x, g, auc, _ = cumulative_gain_curve(df, s, steps=80, normalize=True)
aucs[s] = auc
plt.plot(x, g, label=f"{s} (AUC={auc:.4f})")
plt.axhline(0, linestyle="--", color="black", label="ATE baseline (normalized)")
plt.xlabel("Top % of population (ranked by score)")
plt.ylabel("Normalized cumulative gain")
plt.title(title)
plt.legend()
plt.show()
return aucs
PART A — MARKETING (Bank Marketing)
We now run the full pipeline: 1) load dataset (real or fallback) 2) convert label to 0/1 3) simulate treatment + heterogeneity 4) compute scores 5) evaluate with chapter plots
X_bank, y_bank_raw, bank_source = load_openml_or_fallback("bank-marketing", seed=1)
print("Bank data source:", bank_source)
y_bank_str = y_bank_raw.astype(str).str.lower()
y_bank = y_bank_str.isin(["yes", "1", "true"]).astype(int)
bank_df = simulate_uplift_problem(X_bank, y_bank, seed=11)
bank_scored = add_scores(bank_df, seed=111)
print("Outcome rate:", bank_scored["y"].mean())
print("Treatment rate:", bank_scored["t"].mean())
print("ATE:", effect_binary(bank_scored))
Bank data source: openml
Outcome rate: 0.8868638163278848
Treatment rate: 0.4281037800535268
ATE: 0.06168106138306939
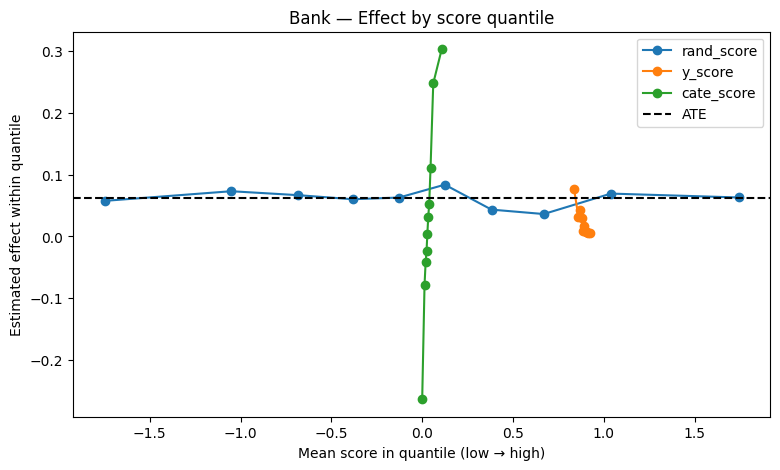
A1) Effect by quantile (marketing)
A strong cate_score should show a clearer upward trend than rand_score.
plot_effect_by_quantile(bank_scored, title="Bank — Effect by score quantile")
A2) Cumulative effect & gain (marketing)
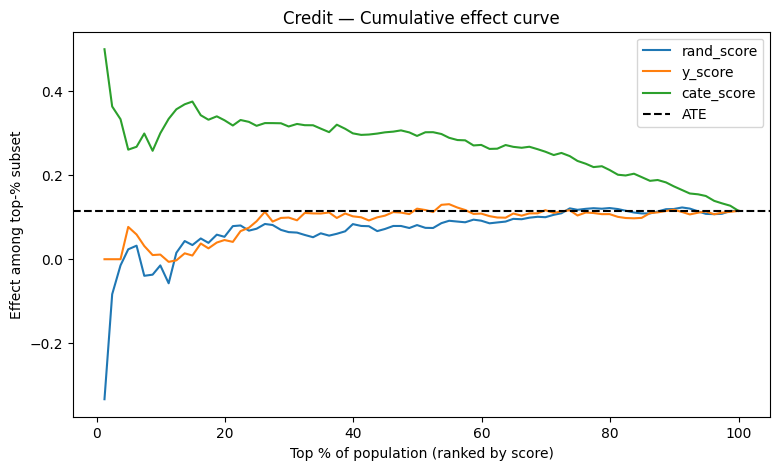
- Cumulative effect: “If I treat top p%, what uplift do I get among those treated?”
- Cumulative gain: downweights tiny p% slices and yields a stable AUC metric.
plot_cumulative_effect(bank_scored, title="Bank — Cumulative effect curve")
bank_aucs = plot_cumulative_gain(bank_scored, title="Bank — Normalized cumulative gain (AUC)")
bank_aucs


{'rand_score': np.float64(-0.0008504006781834974),
'y_score': np.float64(-0.017501049915101506),
'cate_score': np.float64(0.047550307185826986)}
PART B — CREDIT (German Credit / credit-g)
Same pipeline, different domain.
X_credit, y_credit_raw, credit_source = load_openml_or_fallback("credit-g", seed=2)
print("Credit data source:", credit_source)
y_credit_str = y_credit_raw.astype(str).str.lower()
y_credit = y_credit_str.isin(["good", "1", "true", "yes"]).astype(int)
credit_df = simulate_uplift_problem(X_credit, y_credit, seed=22)
credit_scored = add_scores(credit_df, seed=222)
print("Outcome rate:", credit_scored["y"].mean())
print("Treatment rate:", credit_scored["t"].mean())
print("ATE:", effect_binary(credit_scored))
C:\Users\revan\minicondanew\Lib\site-packages\sklearn\datasets\_openml.py:328: UserWarning: Multiple active versions of the dataset matching the name credit-g exist. Versions may be fundamentally different, returning version 1. Available versions:
- version 1, status: active
url: https://www.openml.org/search?type=data&id=31
- version 2, status: active
url: https://www.openml.org/search?type=data&id=44096
warn(warning_msg)
Credit data source: openml
Outcome rate: 0.753
Treatment rate: 0.564
ATE: 0.11511809486628932
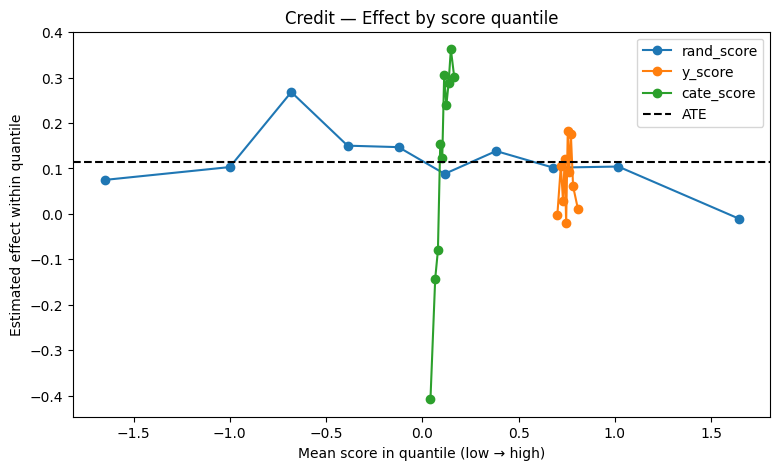
plot_effect_by_quantile(credit_scored, title="Credit — Effect by score quantile")
plot_cumulative_effect(credit_scored, title="Credit — Cumulative effect curve")
credit_aucs = plot_cumulative_gain(credit_scored, title="Credit — Normalized cumulative gain (AUC)")
credit_aucs
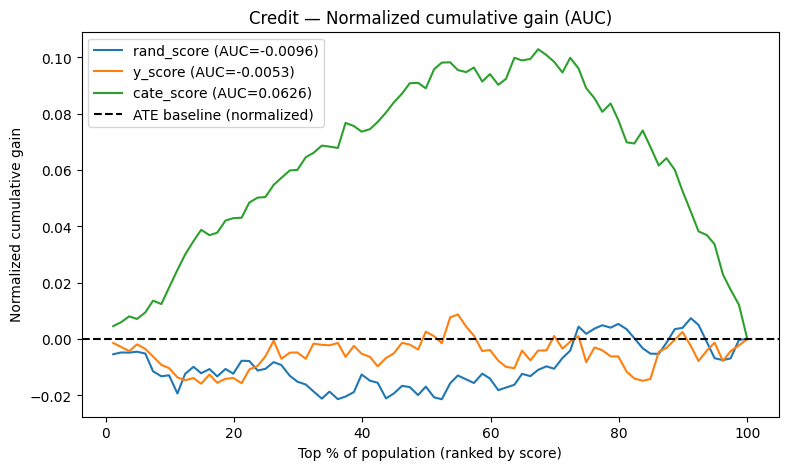
{'rand_score': np.float64(-0.009579854195870837),
'y_score': np.float64(-0.005322435287123906),
'cate_score': np.float64(0.06258574066502405)}
PART C — Target transformation (pseudo-outcome) + weighted MSE
We compute a pseudo-outcome and use it to get a weighted MSE score for each model.
def pseudo_outcome_wmse_report(df: pd.DataFrame):
y = df["y"].values.astype(float)
t = df["t"].values.astype(float)
e = df["e_hat"].values.astype(float)
tau_tilde = pseudo_outcome_transformed(y, t, e, clip=1e-3)
e_clip = np.clip(e, 1e-3, 1 - 1e-3)
w = e_clip * (1 - e_clip)
scores = {
"rand_score": df["rand_score"].values.astype(float),
"y_score": df["y_score"].values.astype(float),
"cate_score": df["cate_score"].values.astype(float),
}
return {k: weighted_mse(tau_tilde, v, w) for k, v in scores.items()}
print("Bank pseudo-outcome weighted MSE:", pseudo_outcome_wmse_report(bank_scored))
print("Credit pseudo-outcome weighted MSE:", pseudo_outcome_wmse_report(credit_scored))
Bank pseudo-outcome weighted MSE: {'rand_score': np.float64(4.944346175875895), 'y_score': np.float64(4.637766410428871), 'cate_score': np.float64(3.926534698283044)}
Credit pseudo-outcome weighted MSE: {'rand_score': np.float64(4.3827211075593295), 'y_score': np.float64(3.8825831197706777), 'cate_score': np.float64(3.4307246359223136)}
Final recap
You now have a single notebook that:
- Uses marketing + credit contexts
- Implements all evaluation plots from the chapter 6 of Facure
- Is runnable even if OpenML is blocked
- Provides clear figures + interpretation